Wild Card Matching

题目

Wild Card Matchin

Given an input string (s) and a pattern (p), implement wildcard pattern matching with support for ‘?’ and ‘*’.

‘?’ Matches any single character.
‘*’ Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).

Note:

s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like ? or *.

Example 1:

Input:
s = "aa"
p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".

Example 2:

Input:
s = "aa"
p = "*"
Output: true
Explanation: '*' matches any sequence.

Example 3:

Input:
s = "cb"
p = "?a"
Output: false
Explanation: '?' matches 'c', but the second letter is 'a', which does not match 'b'.

Example 4:

Input:
s = "adceb"
p = "*a*b"
Output: true
Explanation: The first '*' matches the empty sequence, while the second '*' matches the substring "dce".

Example 5:

Input:
s = "acdcb"
p = "a*c?b"
Output: false

解题报告

理解题意

• 2 个 字符串，长度可能不相等，一个输入字符串，一个是模式字符串
• ? 表示匹配任意单一字符串
• * 表示匹配任意字符串序列（包含空字符串）
• 对完整的输入字符串匹配
• 输入的还有：小写字母 或者空字符

理解例子

• aa 与 a ，单独的 a 不能完整匹配 aa
• aa 与 * ，* 可以匹配任意字符串
• cb 与 ?a, 从后往前看 a 和 b 并不匹配
• abceb 与 *a*b 如下图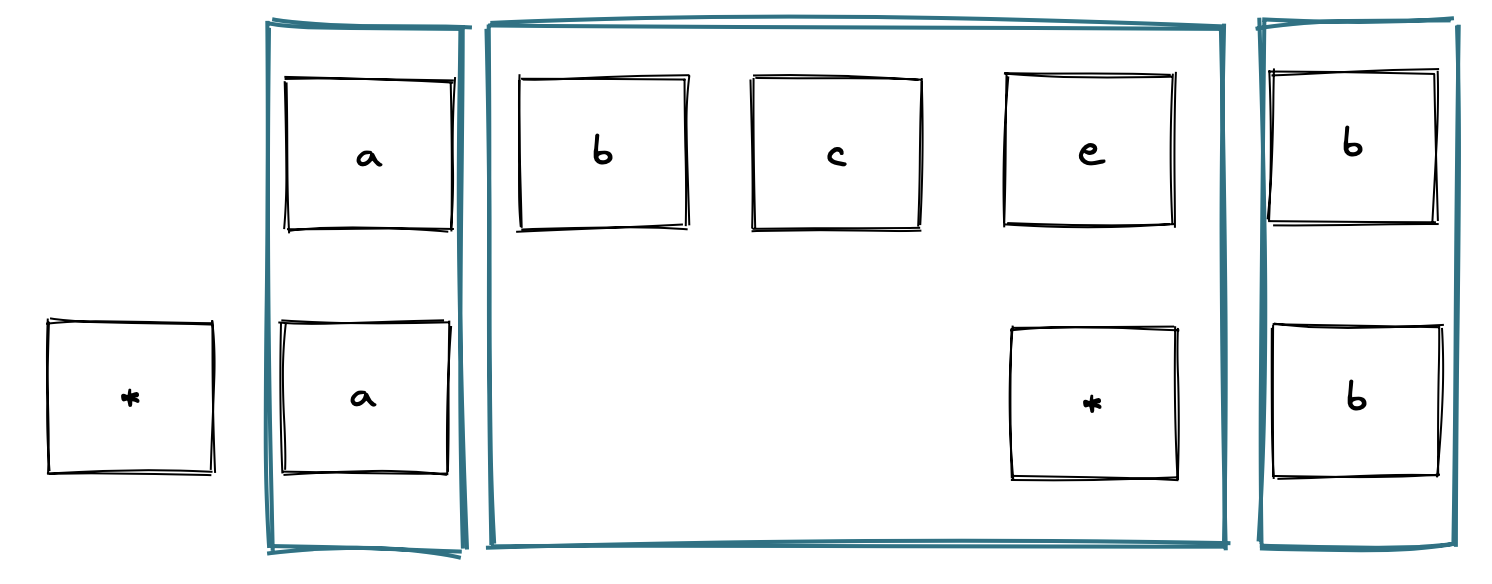
  
• acdcb 与 a*c?b 如下图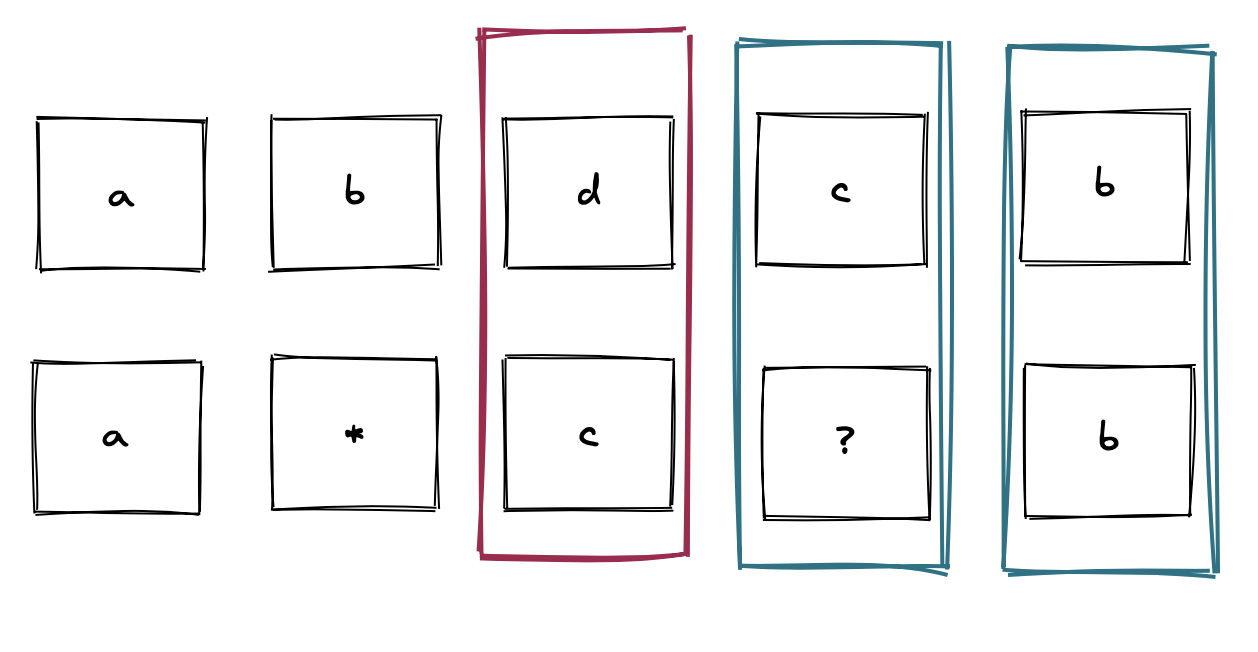
  

思路

• 碰到字符且模式串也是字符，直接比较就行
• 碰到 ? 跳过往前匹配即可，? 就表示匹配，
• 碰到 * 会比较麻烦，因为会匹配 >= 0个字符
• 但一般这种类型的题目可以使用动态规划来解决

代码

Dynamic Programming

• 假定dp_[i][j] 表示 匹配串(长为 i) s[0..i-1] 与模式串(长为 j) p[0..j-1] 是否匹配，
• 首先什么都没有肯定是相互匹配的，那么 dp_[0][0] = true
• dp_[1...i-1][0] = false 表示什么都没有和字符串不匹配
• dp_[0][j] = dp_[0][j-1] 如果 p[j-1] == *

class Solution {
public:
    bool isMatching(string s, string p) {
        const int m = s.length();
        const int n = s.length();
        vector<vector<bool>> dp_ (m+1, vector<bool>(n+1, false));
        dp_[0][0] = true;
        // for (int i = 1; i <= m; i++) {
        //     dp_[i][0] = false;
        // }
        for (int i = 1; i <= n; i++) {
            dp_[0][j] = dp[0][j-1] && (p[j-1] == '*');
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if(p[j-1] == '*') {
                    dp[i][j] = dp_[i][j-1] || dp_[i-1][j];
                } else {
                    dp_[i][j] = dp_[i-1][j-1] && (s[i-1] == p[j-1] || p[j-1] == '?');
                }
            }
        }
        return dp_[i][j];
    }
};

递归

时间复杂度

O(m*n)

空间复杂度

O(m*n)