DynamicProgramming
动态规划套路
有一个 m*n 大小的矩阵迷宫,每次移动只能向右或者向下,文聪左上角到右下角有多少种不同的走法
暴力解法
- 从
(1,1)->(m,n)的不同路径中有大量的重复,比如(1,1)->(i,j)有k条不同的路径,那么对于任何一条固定的路线(i,j)->(m,n)的路径,都需要走k遍来模拟。 - 不关心具体的走法,只关心状态,也就是走法的数量
- 同理,如果知道
(i,j)->(m,n)有k条不同的路径,那么(1,1)->(i,j)->(m,n)的不同路径总数是k*s
动态规划
- 令
(i,j)表示从(1,1)->(i,j)的不同路径数量,f(i,j) = f(i-1,j) + f(i,j-1) - 如果要求出
f(i,j)只需要上一个结果即可, 也就是求解f(i,j)需要求出子问题f(i',j')
动态规划适用前提
无后效性
- 一旦确定
f(i,j),就不用关心如何计算出f(i,j) - 想要确定
f(i,j),只要知道f(i-1,j)和f(i,j-1)
最优子结构
f(i,j)的定义已经蕴含最优- 大问题的最优解可以由若干小问题的最优解推出
(min, max, sum)DP 适用的问题:可以将大问题拆成几个小问题,且无后效性,具有最优子结构的性质
记忆化递归
- 可以使用递归求解
- 有重复子问题,overlaping subproblem
套路一:基本类型(时间序列)
House Robber
- 给一排房子,相邻的房子不能抢,问最多能抢的价值
- 房子只有抢和不抢两个状态
- 和时间相关的为第
i轮
1 | |
House Robber II
- 给一圈“首尾相连”的房子,相邻的房子不能抢,问最多能抢的价值
- 假定有 n 个房子,因为 0 和 n-1 为相邻的房子。因此可抢的范围为
0 -> n-2或者1 -> n-1 - 因此结果就是两个中最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int rob(vector<int>& houses) {
const int m = nums.size();
if (m < 2) return m ? nums[0] : 0;
function<int(int,int)> robHelper = [&](int l, int r){
vector<vector<int>> dp(m+1, vector<int>(2, 0));
dp[l][1] = nums[l];
for (int i = l; i <= r; i++) {
if (i == 0) continue;
dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
dp[i][1] = dp[i-1][0] + nums[i];
}
return max(dp[r][0], dp[r][1]);
};
return max(robHelper(1, m-1), robHelper(0, m-2));
}
};
Best Time to Buy and Sell Stock III
- 给定一系列每日股票的价格,每日只能买入、卖出、不操作。最多交易两次,问最大的收益
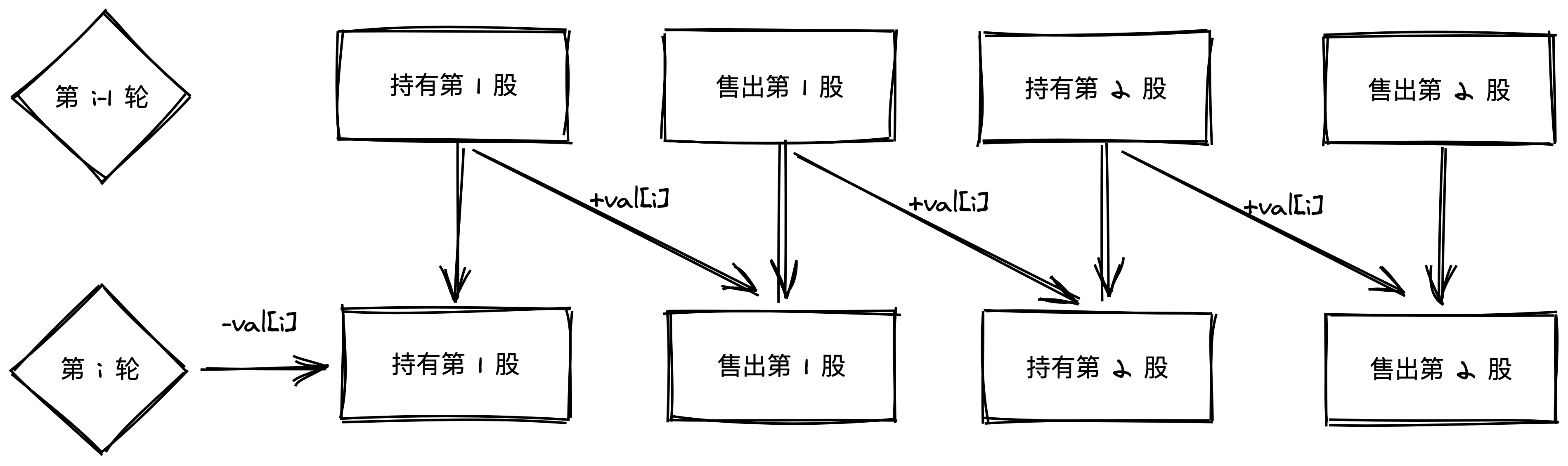
1 | |
Best Time to buy and Sell Stock with cooldown
- 给定一系列股票的加个,每日只能买入、卖出、不操作。买入后要隔卖出,无总交易限制,问最大收益
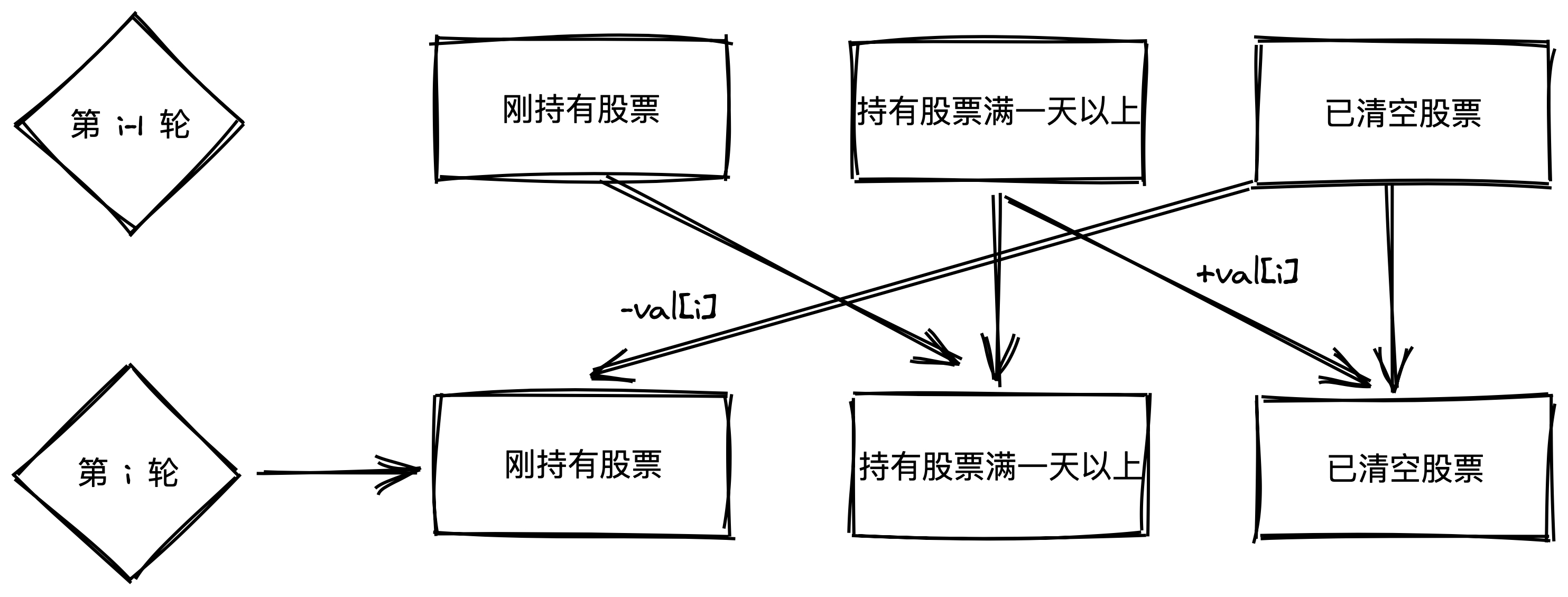
1
2
3
4
5
6
7
8
9
10
11/*
0 表示本轮刚持有股票的最大收益
1 表示本轮持有一天以上的最大收益
2 表示我已清空股票的最大收益
*/
for(int i = 1; i <= n; i++) {
dp[i][0] = dp[i-1][2] - val[i];
dp[i][1] = max(dp[i-1][1], dp[i-1][0]);
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + val[i]);
}
ans = max{dp[i][n]} (n = 1, 2, 3)
Wiggle Subsequence
- 给定一个序列
s, 求其最长的wiggle pattern subsequence (.... >s[i] < s[j] > s[j+1]...)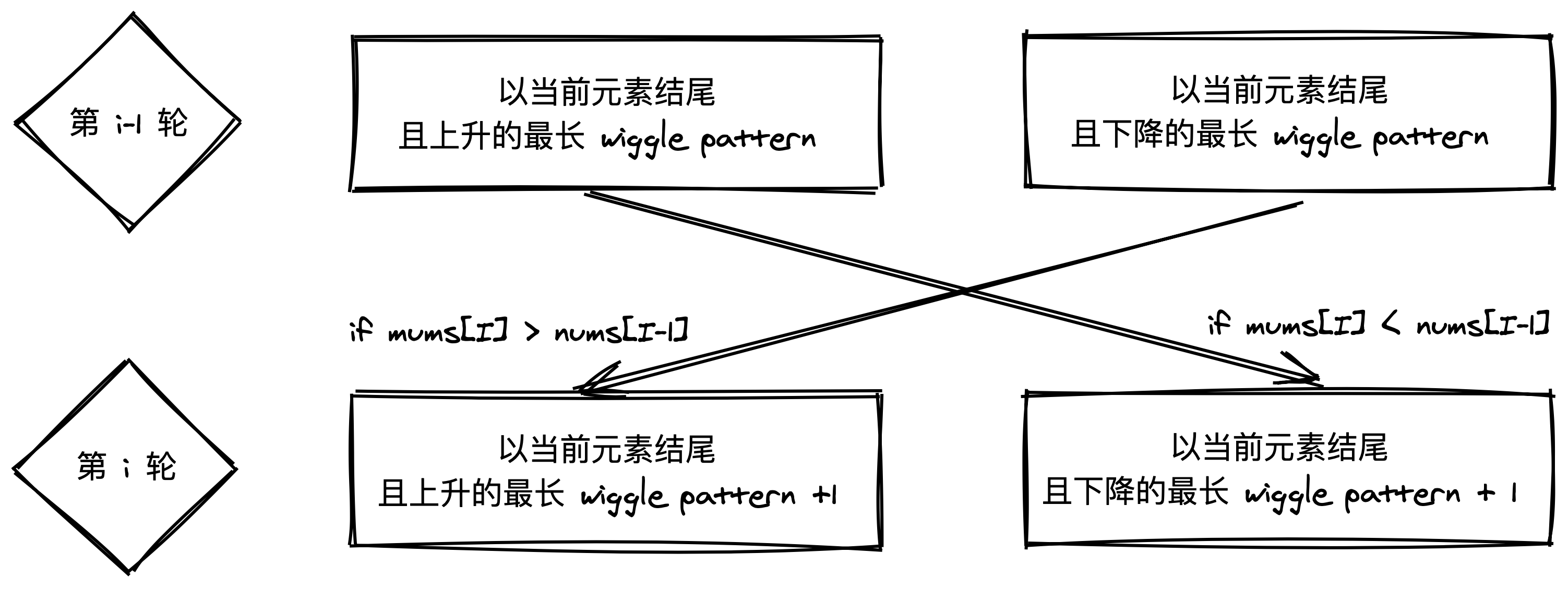
1 | |
Paint Fence
- 给出
cost[i]表示第i个房子喷涂第j中 漆的价格,相邻的房子不能涂同一种颜色,求喷涂所有房子的最小价格

1 | |
To Do or Not To Do
很多不那么套路的 DP 题目,状态比较难以设计,某些题目会给你“行使某种策略的权利”,想买卖股票的题目,两个状态就分别为“行驶了某种权利”,“没有行使某种权利” 分别对应的价值
Max Consecutive One II
- 给定一个数组
(0/1),有最多一次从0翻转到1的权利,问最多可以有多少连续的1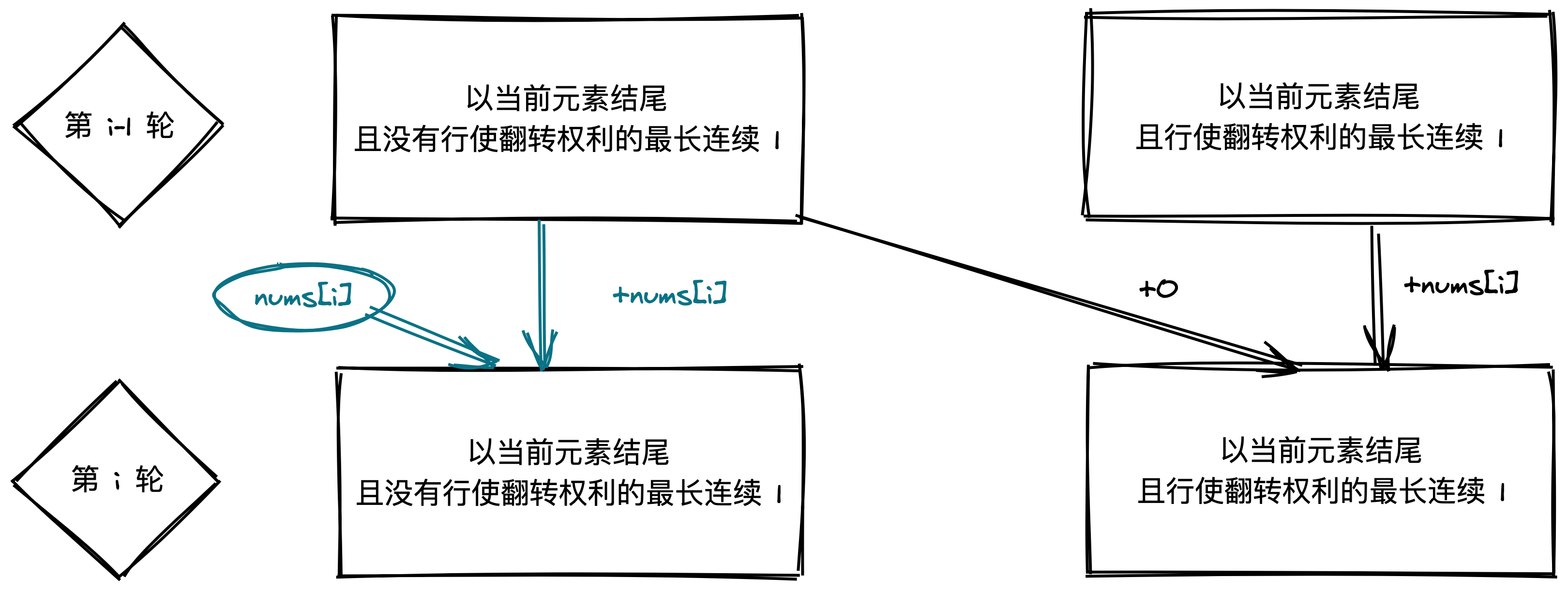
1 | |
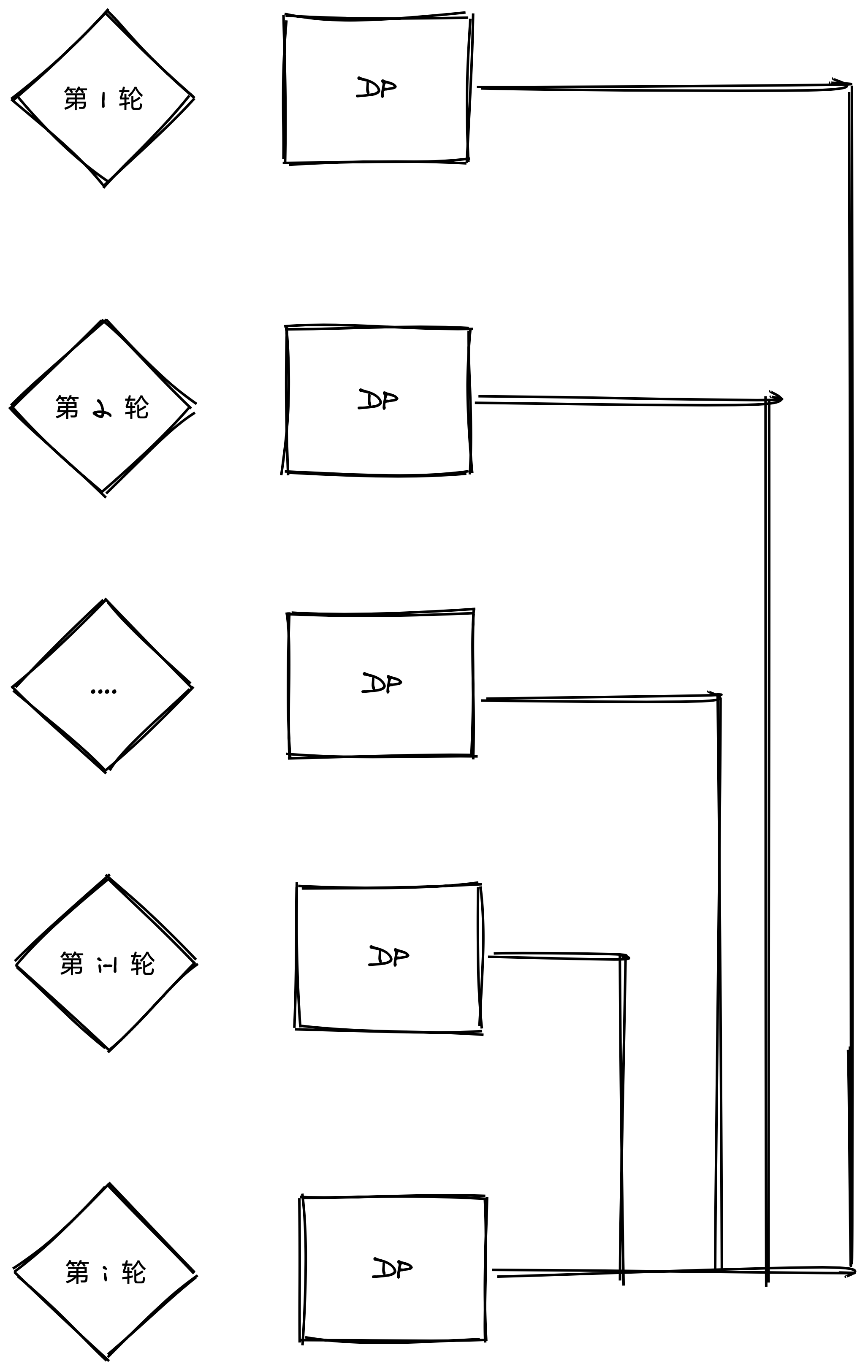
套路二:基本类型 II(时间序列加强版)
- 给定一个序列(数组/字符串),其中每个元素可以认为一天,但今天的状态和之前的某一天有关,需要挑选。
- 套路
定义 dp[i] 表示第 i 轮的状态,一般这个状态要求和元素 i 直接有关系。
千方百计将 dp[i] 与之前的状态 dp[i’] 产生关系比如 sum,max,min,
dp[i] 一定不能与大于 i 的轮次有关系,否则违反了 DP 的无后效性。
- 最终的结果是 dp[i] 中的某一个
Longest Increasing Subsequence
- 给定一个数组 s,求最长的递增子序列的长度
状态定义: 照抄问题,dp[i]–> s[1:i]里面以 s[i]为结尾的、最长的递增子序列的长度。
状态转移:寻找最优解的前驱状态 j,将 dp[i] 与 dp[j] 产生联系
1 | |
Largest Divisible Subset
- 给定一个数组
s,求最大子集,使得里面的所有元素之间都可以相互整除。
状态定义:照抄问题,dp[i]–> s[1:i] 以 s[i]为结尾,满足题目要求的最大子集的数目。
状态转移:寻找最优的前驱状态 j,将 dp[i] 与 dp[j] 产生联系
1 | |
Filling Bookcase Shelves
- 给定
N本书(宽高各异)的序列要求按照所给的顺序摆放,相邻的若干本书可以放一层,但同一层的高度不能超过w。问这个书架最矮可以有多高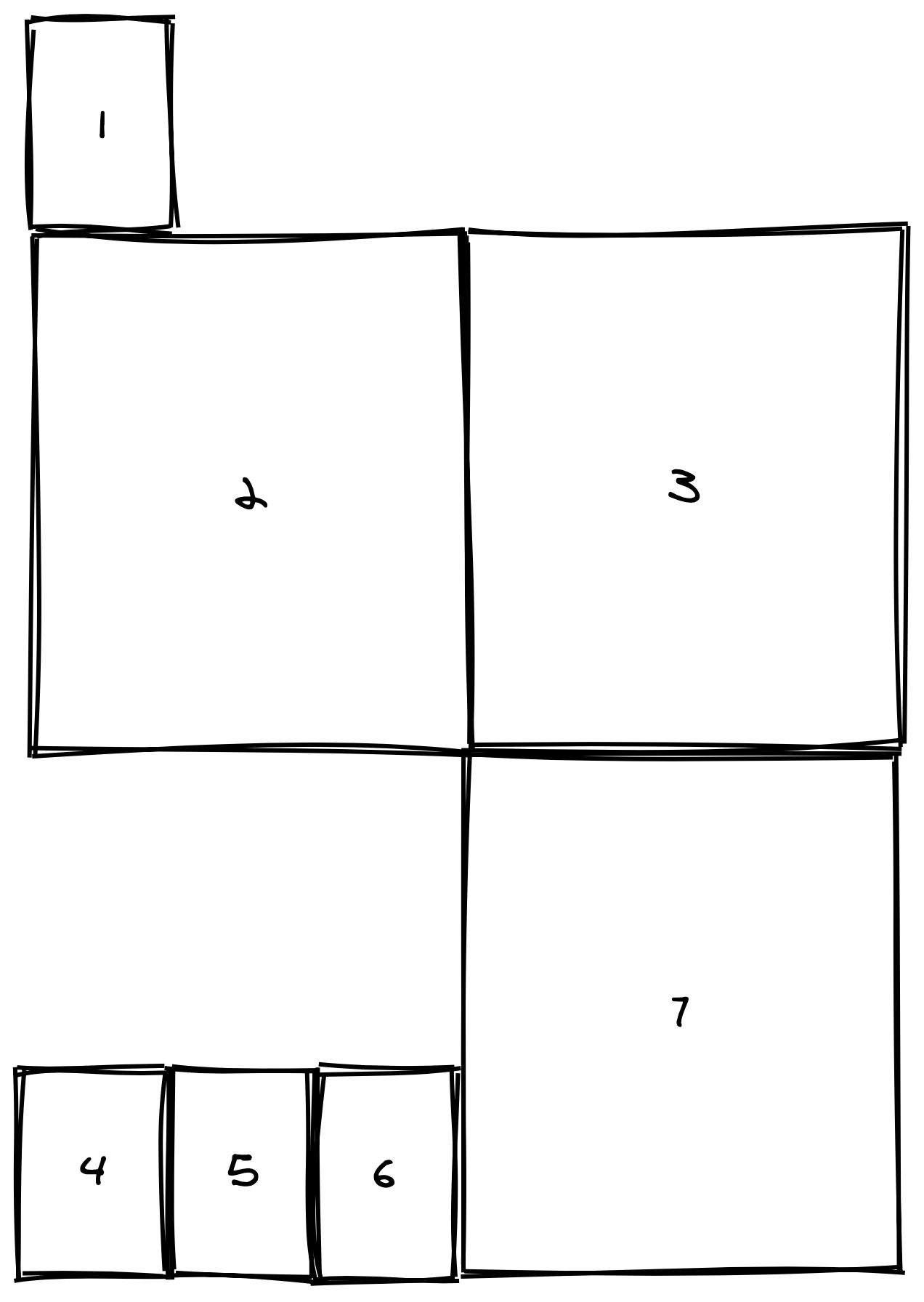
- 将数组 S 分成若干个子数组,最小化“每个数组的最大值之和”,输出该值
状态定义:照抄问题 dp[i]–>将数组S[1,…N] 分成若干个子数组,最小化“每个子数组的最大值之和”,保存该值
状态转移:寻找最优的前驱状态 j,将 dp[i] 与 dp[j] 产生联系
第 i 本书所在的这一层可能有多高?取决于上一层的最后一本书放在那里
1 | |
套路三:双序列类型
- 给出两个序列
s和t(数组/字符串),对他们搞事情 - 套路
定义 dp[i][j]: 表示针对 s[1:i] 和 t[1:j] 的子问题求解答
千方百计将 dp[i][j] 与之前的状态之间转移 dp[i-1][j], dp[i][j-1] , dp[i-1][j-1]
最终的结果是 dp[m][n]
Longest Common subsequences
- 求字符串 s 和 t 的 length of LCS
状态定义:照抄问题 dp[i][j]–> s[1:i] t[1:j]的 length of LCS
状态转移:外面两大层循环编译 i 和 j,核心从 s[i] 与 t[j] 的关系作为突破口,往 dp[i-1][j], dp[i][j-1], dpp[i-1][j] 转移
1 | |
Shortest Common Supersequence
- 求字符串
s和t的length of SCS
状态定义:照抄问题 dp[i][j]–> s[1:i] 和 t[1:j] 的 length of SCS
状态转移:外面两层大循环遍历 i 和 j :核心从 s[i] 与 t[j] 的关系作为突破口,拼命往 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 转移
1 | |
Edit Distance
- 求字符串
s和t的min edit distance
状态定义:照抄问题 dp[i][j]–> s[1:i] 和 t[1:j] 的 min edit distance
状态转移:外面两层大循环遍历 i 和 j :核心从 s[i] 与 t[j] 的关系作为突破口,拼命往 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 转移
套路四:第一类区间类型
套路五:第二类取件类型
套路六:背包入门
状态压缩
DynamicProgramming
https://bapuqln-blog.pages.dev/2020/06/04/DynamicProgramming/

